DISTRIBUCIONES DE FRECUENCIA
La distribución
de frecuencias o tabla de frecuencias es una ordenación en
forma de tabla de los datos estadísticos, asignando a cada dato
su frecuencia correspondiente.
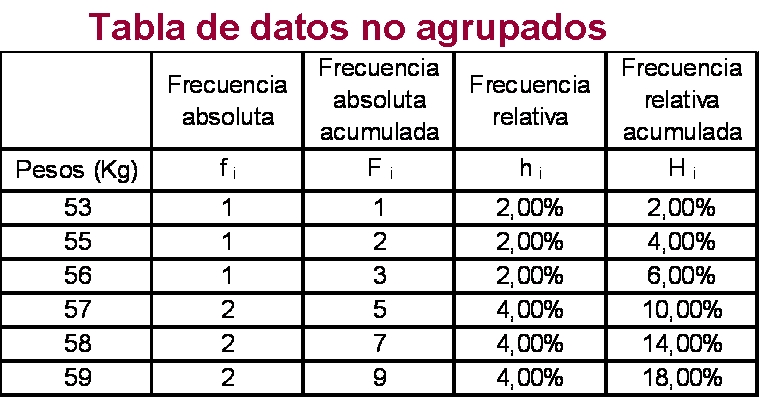
Tipos de frecuencias
Frecuencia absoluta
La frecuencia
absoluta es el número de veces que aparece un determinado valor
en un estudio estadístico.
Se
representa por fi.
La suma
de las frecuencias absolutas es igual al número total de datos, que se
representa por N.
Para
indicar resumidamente estas sumas se utiliza la letra griega Σ (sigma
mayúscula) que se lee suma o sumatoria
Frecuencia relativa
Frecuencia acumulada
Frecuencia relativa acumulada

EJEMPLO:
Durante
el mes de julio, en una ciudad se han registrado las siguientes temperaturas
máximas:
32, 31,
28, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30, 32, 31, 31, 30, 30, 29, 29, 30,
30, 31, 30, 31, 34, 33, 33, 29, 29.
En la
primera columna de la tabla colocamos la variable ordenada de menor a mayor, en
la segunda hacemos el recuento y en la tercera anotamos la frecuencia absoluta.
xi
|
Recuento
|
fi
|
Fi
|
ni
|
Ni
|
27
|
I
|
1
|
1
|
0.032
|
0.032
|
28
|
II
|
2
|
3
|
0.065
|
0.097
|
29
|
6
|
9
|
0.194
|
0.290
|
|
30
|
7
|
16
|
0.226
|
0.516
|
|
31
|
8
|
24
|
0.258
|
0.774
|
|
32
|
III
|
3
|
27
|
0.097
|
0.871
|
33
|
III
|
3
|
30
|
0.097
|
0.968
|
34
|
I
|
1
|
31
|
0.032
|
1
|
31
|
1
|
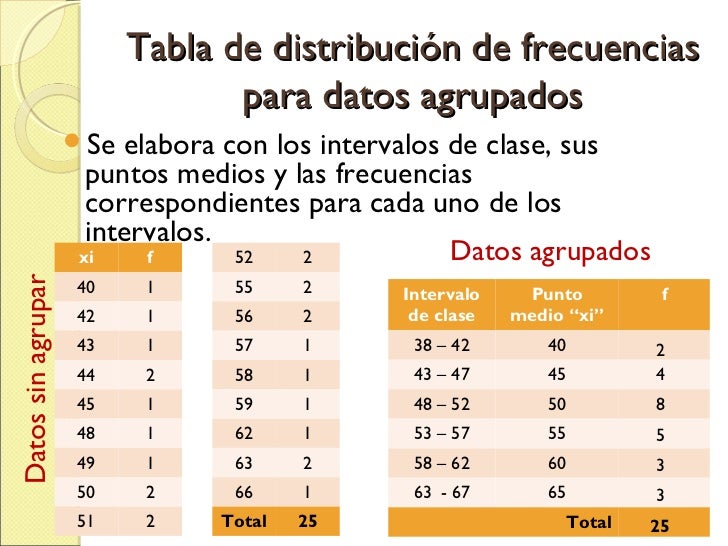
Distribución de frecuencias agrupadas
La distribución
de frecuencias agrupadas o tabla con datos agrupados se emplea si
las variables toman un número grande de valores o la variable
es continua.
Se agrupan
los valores en intervalos que tengan la misma amplitud
denominados clases. A cada clase se le asigna su frecuencia
correspondiente.
Límites de la clase
Cada clase
está delimitada por el límite inferior de la clase y el límite
superior de la clase.
Amplitud de la clase
La amplitud
de la clase es la diferencia entre el límite superior e inferior
de la clase.
Marca de clase
La marca
de clase es el punto medio de cada intervalo y es el valor
que representa a todo el intervalo para el cálculo de algunos parámetros.
Construcción de una tabla de datos agrupados
3, 15,
24, 28, 33, 35, 38, 42, 43, 38, 36, 34, 29, 25, 17, 7, 34, 36, 39, 44, 31, 26,
20, 11, 13, 22, 27, 47, 39, 37, 34, 32, 35, 28, 38, 41, 48, 15, 32, 13.
1º Se
localizan los valores menor y mayor de la distribución. En este caso son 3 y
48.
2º Se
restan y se busca un número entero un poco mayor que la diferencia y que sea
divisible por el número de intervalos queramos establecer.
Es
conveniente que el número de intervalos oscile entre 6 y 15.
En este
caso, 48 - 3 = 45, incrementamos el número hasta 50 : 5 = 10 intervalos.
Se forman
los intervalos teniendo presente que el límite inferior de una clase pertenece
al intervalo, pero el límite superior no pertenece intervalo, se cuenta en el
siguiente intervalo.
ci
|
fi
|
Fi
|
ni
|
Ni
|
|
[0, 5)
|
2.5
|
1
|
1
|
0.025
|
0.025
|
[5, 10)
|
7.5
|
1
|
2
|
0.025
|
0.050
|
[10, 15)
|
12.5
|
3
|
5
|
0.075
|
0.125
|
[15, 20)
|
17.5
|
3
|
8
|
0.075
|
0.200
|
[20, 25)
|
22.5
|
3
|
11
|
0.075
|
0.275
|
[25, 30)
|
27.5
|
6
|
17
|
0.150
|
0.425
|
[30, 35)
|
32.5
|
7
|
24
|
0.175
|
0.600
|
[35, 40)
|
37.5
|
10
|
34
|
0.250
|
0.850
|
[40, 45)
|
42.5
|
4
|
38
|
0.100
|
0.950
|
[45, 50)
|
47.5
|
2
|
40
|
0.050
|
1
|
40
|
1
|
VIDEOS : CONSTRUCCIÓN DE TABLA DE DISTRIBUCIÓN DE FRECUENCIAS PARA DATOS AGRUPADOS.
VIDEO: TABLAS DE DISTRIBUCIÓ DE FRECUENCIA EN EXCELL.
VIDEO: DATOS NO AGRUPADOS.
No hay comentarios.:
Publicar un comentario